Python MRO
在 Python 中,类的方法解析顺序(Method Resolution Order,MRO)是一个是面向对象编程中的重要却又容易被忽视的概念。MRO 定义了类的方法解析顺序,即当一个类的实例调用一个方法时,Python 解释器会按照 MRO 的顺序查找这个方法。本文将介绍 Python 中的 MRO 算法,以及如何使用 C3 算法来计算 MRO。
MRO
在 Python 中,每个类都有一个 MRO 列表,这个列表定义了类的方法解析顺序。MRO 列表是一个有序的类列表,每个类都有一个唯一的位置。当一个类的实例调用一个方法时,Python 解释器会按照 MRO 列表的顺序查找这个方法。
之所以需要 MRO 列表,是因为 Python 支持多重继承。在多重继承中,一个类可以继承多个父类的方法。为了解决多重继承中的方法冲突问题,Python 需要提供一个方法解析顺序,以确定调用哪个方法。
在一般编程实践中,多重继承是一个容易引起混乱的地方,常常是不被推荐的。但是在某些情况下,多重继承是有用的,比如 mixin 模式。在这种情况下,MRO 列表就变得非常重要。
Python 中的 MRO 使用 C3 算法来计算。C3 算法是一种广度优先搜索算法,它可以保证满足多重继承的方法解析顺序。
C3 算法
C3 算法是一种广度优先搜索算法,它可以保证满足多重继承的方法解析顺序。C3 算法的核心思想是:对于一个类的 MRO 列表,它的父类的 MRO 列表必须在它的 MRO 列表之前。
Python 创始人Guido van Rossum这样总结 C3 算法:“基本上,在 C3 背后的想法是,如果你写下在复杂的类层级中继承关系所施加的所有次序规则,这个算法将确定出满足所有这些规则的这些类的一个单调次序。如果不能确定出这样的次序,这个算法会失败。”
C3 算法的过程可以借助 Wikipedia 上的伪代码来理解。下面是一个简单的例子,展示了 C3 算法的过程:
class O
class A extends O
class B extends O
class C extends O
class D extends O
class E extends O
class K1 extends A, B, C
class K2 extends D, B, E
class K3 extends D, A
class Z extends K1, K2, K3
在这个例子中,我们定义了一个类层级,其中包含了多重继承。用图表示这个类层级如下:
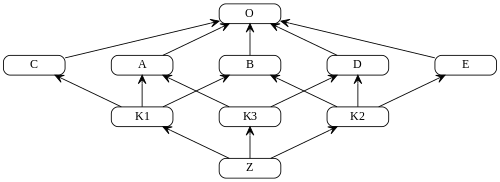
在这个例子中,我们可以使用 C3 算法来计算类 Z 的 MRO 列表。下面是计算过程:
L(O) := [O] // O的线性化就是平凡的单例列表[O],因为O没有父类
L(A) := [A] + merge(L(O), [O]) // A的线性化是A加上它的父类的线性化与父类列表的归并
= [A] + merge([O], [O])
= [A, O] // 其结果是简单的将A前置于它的单一父类的线性化
L(B) := [B, O] // B、C、D和E的线性化的计算类似于A
L(C) := [C, O]
L(D) := [D, O]
L(E) := [E, O]
L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C]) // 首先找到K1的父类的线性化L(A)、L(B)和L(C),接着将它们归并于父类列表[A, B, C]
= [K1] + merge([A, O], [B, O], [C, O], [A, B, C]) // 类A是第一个归并步骤的良好候选者,因为它只出现为第一个和最后一个列表的头部元素。
= [K1, A] + merge([O], [B, O], [C, O], [B, C]) // 类O不是第二个归并步骤的良好候选者,因为它还出现在列表2和列表3的尾部中;但是类B是良好候选者
= [K1, A, B] + merge([O], [O], [C, O], [C]) // 类C是良好候选者;类O仍出现在列表3的尾部中
= [K1, A, B, C] + merge([O], [O], [O]) // 最后,类O是有效候选者,这还竭尽了所有余下的列表
= [K1, A, B, C, O]
L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
= [K2] + merge([D, O], [B, O], [E, O], [D, B, E]) // 选择D
= [K2, D] + merge([O], [B, O], [E, O], [B, E]) // 不选O,选择B
= [K2, D, B] + merge([O], [O], [E, O], [E]) // 不选O,选择E
= [K2, D, B, E] + merge([O], [O], [O]) // 选择O
= [K2, D, B, E, O]
L(K3) := [K3] + merge(L(D), L(A), [D, A])
= [K3] + merge([D, O], [A, O], [D, A]) // 选择D
= [K3, D] + merge([O], [A, O], [A]) // 不选O,选择A
= [K3, D, A] + merge([O], [O]) // 选择O
= [K3, D, A, O]
L(Z) := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])
= [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3]) // 选择K1
= [Z, K1] + merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3]) // 不选A,选择K2
= [Z, K1, K2] + merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3]) // 不选A,不选D,选择K3
= [Z, K1, K2, K3] + merge([A, B, C, O], [D, B, E, O], [D, A, O]) // 不选A,选择D
= [Z, K1, K2, K3, D] + merge([A, B, C, O], [B, E, O], [A, O]) // 选择A
= [Z, K1, K2, K3, D, A] + merge([B, C, O], [B, E, O], [O]) // 选择B
= [Z, K1, K2, K3, D, A, B] + merge([C, O], [E, O], [O]) // 选择C
= [Z, K1, K2, K3, D, A, B, C] + merge([O], [E, O], [O]) // 不选O,选择E
= [Z, K1, K2, K3, D, A, B, C, E] + merge([O], [O], [O]) // 选择O
= [Z, K1, K2, K3, D, A, B, C, E, O] // 完成
从这个例子看出,C3 算法的过程和求拓扑排序有些类似,本质上两者都是通过广度优先搜索来计算一个有序列表。
总结
MRO 是 Python 中的一个重要概念,它定义了类的方法解析顺序。MRO 使用 C3 算法来计算,C3 算法是一种广度优先搜索算法,它可以保证满足多重继承的方法解析顺序。在编写多重继承的代码时,我们需要了解 MRO 的计算过程,以便正确地继承和调用父类的方法。